Blelloch 并行扫描算法

本文是对这篇 博客 的一些补充和 python 代码实现

前缀和 (PrefixSum) 和扫描 (Scan)

在并行计算中，前缀和（prefix sum）被称为“扫描”（scan）主要是因为这个操作的本质涉及对一个序列中的元素进行累积或递推计算，类似于扫描或遍历序列。

其特点是，输出的每一个值有前缀依赖性，就是说每个输出依赖前面的所有输入。

# input:
[a0, a1, a2, a3, ..., an]

# output:
[a0, (a0+a1), (a0+a1+a2), ..., (a0+a1+a2+...+an)]

Blelloch 并行扫描算法

Blelloch 扫描算法（Blelloch scan algorithm）是一种高效并行实现前缀和（prefix sum）操作的算法，通常用于大规模并行计算中。

这个算法采用了一种基于二叉树的并行计算模式, 将传统的 O(n) 求前缀和的复杂度减少为 O(log(n))。

Blelloch 扫描算法由两个主要步骤组成：

1. 向上（Upsweep）阶段：
   • 该阶段是通过一棵隐含的二叉树自底向上构建累积和。
   • 在此过程中，每一个节点汇聚子节点的值。
   • 经过 log(n) 次迭代，最终根节点处存储了整个数组的总和。
2. 向下（Downsweep）阶段：
   • 在这个阶段，算法从树的根节点开始，自顶向下计算前缀和，同时传播累积和到子节点。
   • 在每一层中，左子节点继承父节点的值，而右子节点加上父节点的值。

具体可以参考这个图:

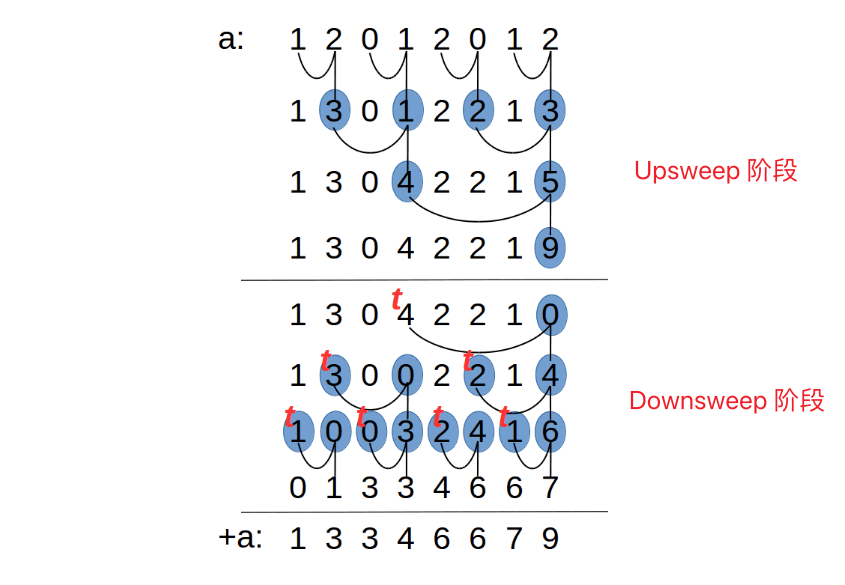
这里用一个 python 代码来展示每一步的具体过程:

def blelloch_scan(arr):
    arr = list(arr)
    n = len(arr)

    print("Initial array:", arr)

    step = 1
    print("\nUpsweep Phase:")
    while step < n:
        for i in range(0, n, 2 * step):
            if i + step < n:
                arr[i + 2 * step - 1] += arr[i + step - 1]
        print(f"After step size {step}, array: {arr}")
        step *= 2

    arr[-1] = 0
    print("\nSetting root to 0, array:", arr)

    step = n // 2
    print("\nDownsweep Phase:")
    while step > 0:
        for i in range(0, n, 2 * step):
            if i + step < n:
                temp = arr[i + step - 1]
                arr[i + step - 1] = arr[i + 2 * step - 1]
                arr[i + 2 * step - 1] += temp
        print(f"After step size {step}, array: {arr}")
        step //= 2

    return arr

input_array = [1,2,0,1,2,0,1,2]
arr = blelloch_scan(input_array)
prefix_sum_array = [input_array[i] + arr[i] for i in range(len(input_array))]

print(f"\nFinal PrefixSum array: {prefix_sum_array}")

输出:

Initial array: [1, 2, 0, 1, 2, 0, 1, 2]

Upsweep Phase:
After step size 1, array: [1, 3, 0, 1, 2, 2, 1, 3]
After step size 2, array: [1, 3, 0, 4, 2, 2, 1, 5]
After step size 4, array: [1, 3, 0, 4, 2, 2, 1, 9]

Setting root to 0, array: [1, 3, 0, 4, 2, 2, 1, 0]

Downsweep Phase:
After step size 4, array: [1, 3, 0, 0, 2, 2, 1, 4]
After step size 2, array: [1, 0, 0, 3, 2, 4, 1, 6]
After step size 1, array: [0, 1, 3, 3, 4, 6, 6, 7]

Final PrefixSum array: [1, 3, 3, 4, 6, 6, 7, 9]

ref

• CUDA-扫描算法 (blog): https://ashburnlee.github.io/2020/02/20/CUDA-扫描算法/
• wikipedia - prefixsum: https://en.wikipedia.org/wiki/Prefix_sum